TEMA-7-TEORÍA DE LA PROBABILIDAD

PROBABILIDAD

El concepto de probabilidad es muy frecuente para comunicarnos y entendernos:

•      Ej: Las probabilidades de sobrevivir a una operación son del 50%
•   Ej: Un paciente que ingresa en el hospital “A” tiene un 15% de padecer una infección hospitalaria
•      Ej: Durante este invierno la prevalencia de enfermedades respiratorias es del 13%. 13 de cada 100 ciudadanos padece una enf. respiratoria durante el invierno.

En todos estos ejemplos se está dando la medida de ocurrencia de un evento que es incierto: sobrevivir a la operación, tener una infección hospitalaria o la ocurrencia de enfermedades respiratorias.

Se expresa mediante un número entre 0 y 1 (o en porcentajes)

En estos ejemplos, si no existe la certeza de que ocurran los hechos, existe una esperanza dimensionada y razonable, de que el hecho anunciado se vea confirmado.

Esta estimación sobre la probabilidad de ocurrencia del evento nos ayuda a tomar decisiones.

Cuanto más probable es que ocurre un evento, su medida de ocurrencia estará más próximo a 1 o al 100% y cuanto menos probable, más se aproxima al cero.

Aunque el concepto es simple, ya que se usa de manera intuitiva, su definición es complicada y tiene tres vertientes:

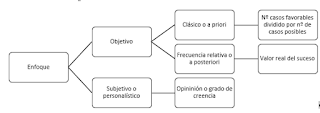
PROBABILIDADES SUBJETIBAS O PERSONALÍSTICAS

La probabilidad mide la confianza que el individuo tiene sobre la certeza de una proposición determinada.

Por ejemplo: los epidemiólogos se basan en la experiencia para afirmar que el próximo invierno la epidemia de gripe tendrá una probabilidad del 0,0018 (180 casos por 100.000 habitantes).

Este concepto de las probabilidades ha dado lugar al enfoque de análisis de datos estadísticos llamado “Estadística Bayesiana”.

PROBABILIDAD CLÁSICA O “A PRIORI”

Data del siglo XVIII (Laplace, Pascal, Fermat), desarrollada para resolver problemas relacionados con los juegos de azar (dados, monedas, ruletas…)

Las probabilidades se calculan con un razonamiento abstracto.

Ejemplo: no hay que lanzar el dado para saber que la probabilidad “a priori” de que salga el 6 es de 1/6=0,16.

Definición: Si un evento puede ocurrir de N formas, las cuales se excluyen mutuamente y son igualmente probables, y si m de esos eventos poseen una característica E, la probabilidad de ocurrencia de E es igual a m/N.

P(E) = 𝒎/N

Ej: La probabilidad “a priori” de que salga un As en una baraja de Póker (52 cartas) será:

·         P(As) = 4/52 = 0,769 = 7,7 %

LEY DE LOS GRANDES NÚMEROS

La probabilidad a priori de que salga un número en el dado es P(A) = 1/6 = 0,166 = 16,6 %

Inicialmente esa probabilidad real puede no cumplirse pero si repetimos muchas veces el experimento, la frecuencia relativa de un suceso A, cualquiera, tiende a estabilizarse en torno al valor “a priori”.

PROBABILIDAD RELATIVA O “A POSTERIORI”

Definición: Si un suceso es repetido un gran número de veces, y si algún evento resultante, con la característica E, ocurre m veces, la frecuencia relativa de la ocurrencia E, m/n, es aproximadamente igual a la probabilidad de ocurrencia de E

P(E) = 𝒎/n

(Si n es suficientemente grande) p = lim fr nà∞

Dicho de otra forma, si el número de determinaciones (repeticiones de un experimento aleatorio) es grande, podemos esperar que la probabilidad observada se acerque a la probabilidad teórica.

EVENTOS O SUCESOS

Diversos resultados son posibles cuando realizamos un experimento aleatorio. El conjunto de estos resultados se llama espacio muestral (S).

Suceso o evento: subconjunto de dichos resultados.

Evento unión: formado por los resultados experimentales que están en A o en B (incluyendo los que están en ambos).

Evento intersección: formado por los elementos que están en A y B.

PROPIEDADES DE LAS PROBABILIDADES

P(AUB): Cuando dos sucesos A y B se excluyen mutuamente: P(AUB)=P(A)+P(B)

P(AUB): Cuando dos sucesos A y B no se excluyen mutuamente: P(AUB)=P(A)+P(B)-P(AПB)

P(AUB): Cuando A y B son eventos independientes (la ocurrencia de uno no influye en la ocurrencia del otro): P(AПB)=P(A)xP(B)

REGLAS BÁSICAS: TEORÍA DE LA PROBABILIDAD

Las probabilidades siempre oscilan entre 0 y 1

La probabilidad de un suceso contrario es igual a 1 menos la probabilidad del suceso – P (A´)= 1-P(A)

La probabilidad de un suceso imposible es 0

La unión de A y B es:

•          P(AUB)=P(A)+P(B)-P(A П B)

La probabilidad condicionada de un suceso A a otro B se expresa:

P (A/B)= P(A П B)/P(B)                                                  Si P(B)=’0

TEOREMA DE BAYES

Expresa la probabilidad condicional de un evento aleatorio A dado B en términos de la distribución de probabilidad condicional del evento B dado A y la distribución de probabilidad marginal de sólo A.

En términos más generales el teorema de Bayes que vincula la probabilidad de A dado B con la probabilidad de B dado A.

Por ejemplo, sabiendo la probabilidad de tener un dolor de cabeza dado que se tiene gripe, se podría saber (si se tiene algún dato más), la probabilidad de tener gripe si se tiene un dolor de cabeza.

DISTRIBUCIÓN DE PROBABILIDAD EN VARIABLES DISCRETAS: BINOMIAL Y 
POISSON

DISTRIBUCIÓN BINOMIAL

La distribución binomial es un modelo matemático de distribución teórica de (la normal es con variables continuas) variables discretas

•         Cuando se producen situaciones en las que sólo existen dos posibilidades (cara/cruz; sano/enfermo…)
•        El resultado obtenido en cada prueba es independiente de los resultados obtenidos anteriormente.
•        La probabilidad del suceso A es constante, la representamos por p, y no varía de una prueba a otra. La probabilidad de `A es 1- p y la representamos por q .
•         El experimento consta de un número n de pruebas.

Mediante esta distribución se resuelven los problemas que plantean:

• Si al hacer un experimento hay una probabilidad p de que ocurra un suceso ¿Cuál es la probabilidad de que en N experimentos el suceso ocurra X veces?

o   P: probabilidad de ocurrencia; q de no ocurrencia

o   X: numero sucesos favorables

o   N: numero total de ensayos

•          Y… recordar que por definición el factorial de un número 0 es igual a 1.

DISTRIBUCIÓN DE POISSON

Poisson: médico miliar francés que estudia en el s.XIX la probabilidad de que un soldado muera en el campo de batalla por golpes de un caballo

•          También se llama la distribución de probabilidad de casos raros

Utilidad:

1. Se utiliza en situaciones dónde los sucesos son impredecibles o de ocurrencia aleatoria.
2. Permite determinar la probabilidad de ocurrencia de un suceso con resultado discreto.
3. Es muy útil cuando la muestra o segmento n es grande y la probabilidad de éxitos p es pequeña.
4. Se utiliza cuando la probabilidad del evento que nos interesa se distribuye dentro de un segmento n dado como por ejemplo distancia, área, volumen o tiempo definido.

DISTRIBUCIONES NORMALES

TIPIFICACIÓN DE VALORES EN UNA NORMAL

Extrapolando aparecen los principios básicos de las distribuciones normales y podemos tipificar valores de una normal:

•          ± 1S 68,26% de las observaciones
•          ± 2S 95,45% de las observaciones
•          ± 1,95S 95% de las observaciones
•          ± 3S 99,73% de las observaciones
•          ± 2,58S 99% de las observaciones

TIPIFICACIÓN DE LOS VALORES Y SU RELACIÓNCON LA CAMPANA DE GAUSS

La tipificación de los valores se puede realizar sí …

Trabajamos con una variable continua que:

•        Sigue una distribución normal (TLC)
•     Y tiene más de 100 unidades (LGN)

La tipificación nos permite conocer si otro valor corresponde o no a esa distribución de frecuencia

Sabemos por la forma de la curva que…

•          La media coincide con lo más alto de la campana: 8
•          La desviación típica es de 2 puntos

o   El 50% tiene puntuaciones>8

o   El 50% tiene puntuaciones<8

o   Aproximadamente el 68% puntúa entre 6 y 10

§  media +/- 1 desviación típica: 68%

·         8+/-1: 6-10

§  Media +/- 2 desviación típica: 95%

·         4-12

§  Media +/- 3 desviación típica: 99%

·         2-14