TEMA-12-CONCORDANCIA Y CORRELACIÓN

ESTUDIO CONJUNTO DE DOS VARIABLES

Una de las formas de recoger los datos obtenidos observando dos variables en varios individuos de una muestra, es en una tabla.

• En las filas tendremos los datos de un individuo.
• En cada columna se representará los valores que toma una variable sobre los mismos.
• Los individuos no se muestran en ningún orden particular.

Dichas observaciones pueden ser representadas en un diagrama de dispersión. En ellos, cada individuo es un punto cuyas coordenadas son los valores de las variables.

Nuestro objetivo será intentar reconocer a partir del mismo si hay relación entre las variables, de qué tipo, y si es posible predecir el valor de una de ellas en función de la otra.

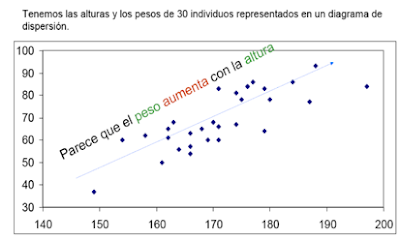
DIAGRAMAS DE DISPERSIÓN O NUBE DE PUNTOS

RELACIÓN ENTRE VARIABLES

PREDICCIÓN DE UNA VARIABLE EN FUNCIÓN DE OTRA

RELACIÓN DIRECTA E INVERSA

Incorrelación: Para valores de X por encima de la media tenemos de Y por encima y por debajo en proporciones similares.

Relación directa: para los valores X mayores que la media le corresponden valores de Y mayores también, y viceversa con ambos.

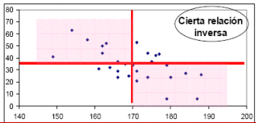
Relación inversa: para los valores de X mayores que la media le corresponden valores de Y menores.

MODELOS DE ANÁLISIS DE REGRESIÓN

REGRESIÓN LINEAL SIMPLE: CORRELACIÓN Y DETERMINACIÓN

•          Se trata de estudiar la asociación lineal entre dos variables cuantitativas
•          Ejemplo: influencia de la edad en las cifras de Tensión arterial Sistólica
•         Regresión lineal simple: una sola variable independiente
•         Regresión lineal múltiple: más de una variable independiente
•         Ecuación de la recta: y = ax + b (ej: TAS=a· edad +b)
•         Pendiente de la recta a = β1
•         Punto de intersección con el eje de coordenadas b=β0
•         Pendiente de la recta a = β1
•         Punto de intersección con el eje de coordenadas b=β0
•     Β1 expresa la cantidad de cambio que se produce en la variable dependiente por unidad de cambio de la variable independiente
•          Β0 expresa cuál es el valor de la variable dependiente cuando la independiente vale cero
•     Modelos lineales deterministas: la variable independiente determine el valor de la variable dependiente. Entonces para cada valor de la variable independiente sólo habría un valor de la dependiente
•    Modelos lineales probabilísticos: Para cada valor de la variable independiente existe una distribución de probabilidad de valores de la dependiente, con una probabilidad entre 0 y 1.
•          La recta a determinar es aquélla con la menor distancia de cada punto a ella.

ANÁLISIS DE CORRELACIÓN

El análisis de correlación se utiliza con el propósito de disponer de un indicador cuantitativo que permite sintetizar el grado de la asociación entre variables.

VARIABLES CUANTITATIVAS NORMALES:

Coeficiente de Correlación r de Pearson: mide el grado de la relación de dependencia que existe entre las variables (x,y), cuyos valores van desde -1, correspondiente a una correlación negativa perfecta, hasta 1, correspondiente a una correlación positiva perfecta.

La magnitud del Coeficiente de Correlación (r) indica cuán cerca están los puntos de la recta, tomando valores entre 1 y -1.

VARIABLES ORDINALES:

El coeficiente de Correlación por Rango de rho de Spearman es una medida de asociación que requiere que ambas variables en estudio sean medidas por lo menos en una escala ordinal.

ALGUNAS DE LAS FORMAS DE COMPROBAR LA NORMALIDAD DE LOS DATOS

• Prueba de Kolmogorov-Smirvov
• Prueba de Shapiro-Wilk

REGRESIÓN LINEAL SIMPLE: CORRELACIÓN Y DETERMINACIÓN

•          Y = β1 · x + β0
•          Yi= β1 · x + β0 + ei
•      Y sería la media de la variable dependiente en un grupo con el mismo valor de la variable independiente Yi= y + ei
•          Para construir un modelo de regresión lineal hace falta conocer: Punto de intersección con el eje de coordenadas=β0 y la Pendiente de la recta a = β1
•          No hay un modelo determinista: hay una nube de puntos y buscamos la recta que mejor explica el comportamiento de la variable dependiente en función de la variable independiente

Teniendo una nube de puntos, ¿cómo elegir la recta que mejor se ajuste a esos puntos?: Mediante el método de los mínimos cuadrados.

Se trata de la recta que hace mínimo el cuadrado de la suma de las distancias verticales desde ella hasta cada uno de los puntos de la nube.

·       Coeficiente de correlación (Pearson y Spearman): Número adimensional (entre -1 y 1) que mide la fuerza y el sentido de la relación lineal entre dos variables.

·         r= β1 • sx /sy

·     Coeficiente de determinación: número adimensional (entre 0 y 1) que dá idea de la relación entre las variables relacionadas linealmente. Es r2

TEMA-11-PRUEBAS NO PARAMÉTRICAS MÁS UTILIZADAS EN ENFERMERÍA

PRUEBAS NO PARAMÉTRICAS:

Análisis bivariado de variables cualitativas: Test de hipótesis Chi-cuadrado

Para comparar dos variables cualitativas (dependiente e independiente)

Razonamiento a seguir: suponemos la hipótesis cierta y estudiamos cómo es de probable que siendo iguales los dos grupos a comparar se obtengan resultados como los obtenidos o haber encontrado diferencias más grandes por grupos

Tablas de contingencia-Frecuencias absolutas

Se emplean para registrar y analizar la asociación entre dos o más variables de naturaleza cualitativa (nominales u ordinales)

Veamos: Tabla de contingencia general para la comparación de dos variables dicotómicas.

Se emplean para registrar y analizar la asociación entre dos o más variables, de naturaleza cualitativa (nominales u ordinales)

Por ejemplo ¿Existen diferencias en el consumo de tabaco en función del sexo?

Lo vemos mejor comparando los porcentajes

Tabla de contingencia-porcentaje

Se emplean para registrar y analizar la asociación entre dos o más variables, habitualmente de naturaleza cualitativa (nominales u ordinales)

Pregunta de investigación: ¿Existe asociación entre el sexo y el consumo de tabaco?

Hipótesis:

•          Ho=No existe asociación entre el sexo y el consumo de tabaco
•          H1=Existe asociación entre el sexo y el consumo de tabaco

PRUEBA CHI-CUADRADO

La prueba o estadístico Chi cuadrado se utiliza para comprobar si la diferencia en los datos que observamos:

•          Es debida al azar

o   Recordemos que la Ho establece que no hay diferencia, que hay igualdad. Aceptamos la Ho

•          Es debida a algo más, por ejemplo una asociación entre las variables que estudiamos.

o   Rechazamos la H0. Aceptamos la H1.

CONDICIONES PARA APLICAR LA CHI CUADRADO

•        Las observaciones deben ser independientes. Es decir, al clasificar los sujetos en cada casilla, debe haber sujetos distintos; no puede haber sujetos repetidos en más de una casilla. Ni los sujetos se pueden clasificar en más de un lugar.
•         Utilizar en variables cualitativas
•         Más de 50 casos
•         Las frecuencias teóricas o esperadas en cada casilla de clasificación no deben ser inferiores a 5
•      Si son menores que 5, no podemos sacar conclusiones del contraste de hipótesis con Chi-cuadrado. Algunos autores señalan como tolerable que un 20% de las casillas tengan una frecuencia teórica inferior a 5, pero no deben ser muy inferiores.

Si no se cumplen los requisitos: Se usan pruebas paramétricas

1)      Utilizar el estadístico de Fisher

2)      Corrección de continuidad de Yates: Actualmente discutido por bastantes autores y se puede no tener en cuenta. Conviene mencionarla porque responde a una práctica muy generalizada y figura en muchos textos.

RECORDEMOS EN LA PRUEBA DE CHI CUADRADO

Frecuencia observada: la que recogen los datos

Frecuencia esperada: la que observaríamos si no hubiera relación

Grados de libertad: Número de valores o datos que pueden variar libremente dado un determinado resultado

Grados de libertad = (filas -1)*(columnas -1) (número de filas menos una) por (número de columnas menos una).

PRUEBA CHI-CUADRADO

Permite determinar si dos variables cualitativas están o no asociadas. Es decir si son dependientes (H1) o independientes (Ho).

Para su cómputo calculamos:

•          Frecuencias esperadas (FE): aquellas que deberían haberse observado si la Ho fuese cierta, ie, si ambas variables fueran independientes
•          Frecuencias observadas (FO) en nuestro estudio.

Las comparamos para calcular el valor del estadístico chi-cuadrado (𝑋 2 ):

Cuanto mayor sea la diferencia (y, por tanto, el valor del estadístico), mayor es la asociación/dependencia entre ambas variables

Por otra parte, como las diferencias entre las frecuencias observadas y esperadas están elevadas al cuadrado, esto hace que el valor de 𝑋 2 siempre sea positivo.

Para obtener los valores esperados, éstos se calculan a través del producto de los valores totales marginales dividido por el número total de casos (n). Para el caso más sencillo de una tabla 2x2:

ODDS RATIO

Permite cuantificar la importancia/fuerza de la asociación entre dos variables

Puede acompañar al resultado de la prueba chi-cuadrado (en variables dicotómicas)

¿Recordamos la odds? Frecuencia expuestos/frecuencia no expuestos (casos y controles)

Odds ratio sería el cociente entre la odds del grupo de individuos de la categoría 1 de la variable supuestamente dependiente (variable 2) (a/c), frente a la odds del otro grupo formado por los individuos de la categoría 2 de esa misma variable (b/d).

Características

•          No tiene dimensiones.
•          El rango va de 0 a ∞
•          OR=1 indica que no hay asociación (independencia)
•      OR>1 la presencia del factor de exposición (V1.1) se asocia a mayor ocurrencia del evento (V2.1)
•     OR<1 la presencia del factor de exposición (V1.1) se asocia a menor ocurrencia del evento (V2.1)

TEMA-10-ESTIMACIÓN Y/O SIGNIFICACIÓN ESTADÍSTICA. DISTRIBUCIONES MUESTRALES PARA MEDIAS Y DATOS CONTINUOS. DISTRIBUCIONES MUESTRALES PARA PROPORCIONES Y DATOS CATEGÓRICOS

SIGNIFICACIÓN ESTADÍSTICA

• Una de las dos formas de inferencia estadística (la otra es la estimación puntual y/o por intervalos)

• Permite contrastar hipótesis y relacionarlo con el método científico

• Se parte de la hipótesis nula, frente a la hipótesis alternativa

• Permite calcular el nivel de significación

• Nos permite tomar decisiones, cuantificando el error

HIPÓTESIS ESTADÍSTICA

•        Es una creencia sobre los parámetros de una o más poblaciones
•        Es una proposición sobre la distribución de probabilidad de una variable
•        Siempre son proposiciones sobre la población, no sobre la muestra
•        Son conjeturas que se hacen antes de empezar el muestreo
•        Pretenden comprobar si las diferencias encontradas en la muestra del estudio se pueden generalizar a la población
•        Para ello se construye un modelo teórico en el que se formula una hipótesis:

             – Hipótesis nula (H0): contempla la no existencia de diferencias entre los parámetros                  que se comparan

             – Hipótesis alternativa (H1): contempla la existencia de diferencias entre los                                parámetros que se comparan

CONTRASTES DE HIPÓTESIS

•     Para controlar los errores aleatorios, además del cálculo de intervalos de confianza, contamos con una segunda herramienta en el proceso de inferencia estadística: los tests o contrastes de hipótesis
•      Con los intervalos nos hacemos una idea de un parámetro de una población dando un par de números entre los que confiamos que esté el valor desconocido
•        Con los contrastes (tests) de hipótesis la estrategia es la siguiente:

–  Establecemos a priori una hipótesis acerca del valor del parámetro

–  Realizamos la recogida de datos

–  Analizamos la coherencia de entre la hipótesis previa y los datos obtenidos

•    Son herramientas estadísticas para responder a preguntas de investigación: permite cuantificar la compatibilidad entre una hipótesis previamente establecida y los resultados obtenidos
•     Sean cuales sean los deseos de los investigadores, el test de hipótesis siempre va a contrastar la hipótesis nula (la que establece igualdad entre los grupos a comparar, o lo que es lo mismo, la no que no establece relación entre las variables de estudio)
•     Se utiliza la prueba estadística correspondiente y se mide la probabilidad de error al rechazar la hipótesis nula, asociada al valor de p
•      Según el nivel de significación que hayamos preestablecido (habitualmente un 95%) las soluciones pueden ser:

                        - p>0,05: en este caso no podemos rechazar la hipótesis nula (no podemos decir                          que sea cierta, sino que no podemos rechazarla)

                         -p<0,05: en este caso rechazamos la hipótesis nula, por lo que debemos aceptar la                                  hipótesis la hipótesis alternativa.

ERRORES DE HIPÓTESIS

•        Con una misma muestra podemos aceptar o rechazar la hipótesis nula, todo depende de un error, al que llamamos α
•       El error α es la probabilidad de equivocarnos al rechazar la hipótesis nula
•       El error α más pequeño al que podemos rechazar H0 es el error p
•       Habitualmente rechazamos H0 para un nivel α máximo del 5% (p<0,05) 
•       Es lo que llamamos “significación estadística”

TEMA-8-TEORÍA DE MUESTRAS

ESTIMACIÓN E INFERENCIA ESTADÍSTICA

Al conjunto de procedimientos que permiten elegir muestras de tal forma que éstas reflejan las características de la población le llamamos técnicas de muestreo.

Siempre que trabajamos con muestras (no estudiamos el problema en toda la población sino en una parte de ella) hay que asumir un cierto error.

Si la muestra se elige por un procedimiento de azar, se puede evaluar un error. La técnica de muestreo en ese caso se denomina muestreo probabilístico o aleatorio y el error asociado a esa muestra elegida al azar se llama error aleatorio.

En los muestreos no probabilísticos no es posible evaluar el error. En los muestreos probabilísticos, el error aleatorio es inevitable, pero es evaluable.

Proceso de inferencia: quiero medir un parámetro, no lo puedo medir en todos los sujetos, realizo una selección preferiblemente aleatoria, una muestra mediante muestreo, calculo estimador de ese parámetro y a partir del estimador hago la inferencia, es decir, puedo aproximarme al conocimiento del parámetro.

PROCEDIMIENTO MUESTRAL O TÉCNICA DE MUESTREO

Un muestreo es un método tal que al escoger un grupo pequeño de una población podamos tener un grado de probabilidad de que ese pequeño grupo posea las características de la población que estamos estudiando. Tenemos que tener en cuenta además de la técnica el tamaño.

• El tamaño de la muestra a tomar va a depender de:
• El error aleatorio (estándar)
• De la mínima diferencia entre los grupos de comparación que se considera importante en los valores de la variable a estudiar
• De la variabilidad de la variable a estudiar (varianza en la población)
• El tamaño de la población del estudio.

Cálculo del tamaño de la muestra para estimar la media de una población: el tamaño de población que tengo que escoger es:

n= z² x S² / e²

•    Z es el valor que depende del nivel de confianza 1-α con que se quiera dar a los intervalos calculados a partir de estimadores de esa muestra (Para nivel de confianza 95% z= 1,96 y para el nivel de confianza 99% z= 2,58)
•    S² es la varianza poblacional
•    e es el error máximo aceptado por los investigadores en las diferencias entre los grupos de comparación de la variable a estudiar, es decir, en cuantos puntos quiero equivocarme en 1, 2, 3…
•    Si tras esta operación se cumple el resultado: N>n (n- 1). El cálculo del tamaño termina.
•    Si no se cumple, obtendremos el tamaño de la muestra con esta fórmula n’= n/ 1 + (n/N)

Para calcular el tamaño de una muestra cuando queremos estimar una proporción:

•  P es la proporción de una categoría de la variable (si presencia de la enfermedad
•  1-p la proporción de la otra categoría (no tengo la enfermedad)
•  Z valor que depende del nivel de confianza 1-α
•  N es el tamaño de la población
•  e es el error máximo aceptado por los investigadores en las diferencias entre los grupos de comparación de las variables a estudiar.

Tipos de muestreo

•     No probabilístico: son los peores porque no utilizan el azar y siempre hay un sesgo de selección (tú lo seleccionas). No sigue proceso aleatorio y no puede considerarse que la muestra sea representativa de una población. Se caracteriza porque el investigador selecciona la muestra siguiendo algunos criterios identificados para los fines del estudio que realiza. Entre ellos encontramos:

o Por conveniencia o Internacional: el investigador decide, según sus objetivos, los elementos que integrarán la muestra considerando las unidades “típicas” de la población que desea conocer.

o   Por cuotas (es una variante del de conveniencia): el investigador selecciona la muestra considerando algunos fenómenos o variables a estudiar, como: sexo, raza, religión etc.

o   Accidental: consiste en utilizar para el estudio las personas disponibles en un momento dado, según lo que interesa estudiar. De las tres es la peor. Por ejemplo, ir a una biblioteca a medir el perfil del estudiante general.

•       Probabilísticos: introducen el azar, por lo que me ayuda a saber con qué fiabilidad puedo hacer la inferencia. Todos y cada uno de los elementos tienen una probabilidad calculable y por lo tanto, conocida, de ser elegidas para la muestra. Consiste en extraer una parte (o muestra) de una población o universo, de tal forma que todas las muestras posibles de tamaño fijo, tengan la misma posibilidad de ser seleccionadas.

o   Por conglomerado: es el menos fiable. Si no disponemos de una lista detallada enumerada de cada una de las unidades que conforman el universo y resulta muy complejo elaborarla. En la selección de la muestra en lugar de escogerse cada unidad se toman los subgrupos conjuntos de unidades “conglomerados”. No conoce el investigador la distribución variable y las inferencias no son tan confiables como las de muestreo aleatorio.

o   Estratificados: se caracteriza por la subdivisión de la población en subgrupos o estratos, debido a que las variables principales que deben someterse a estudio presentan cierta variabilidad o distribución conocida que puede afectar a los resultados. Por ejemplo, tengo una población de 250 habitantes (N=250) y quiero seleccionar a 50 (n=50), averiguo que distribución por sexo hay en la población (180 mujeres y 70 hombres en enfermería, un porcentaje de 72% de mujeres y un 28% de varones) y forzamos ese mismo porcentaje en la población selecciona (en la de 50) y habría entonces de esos 50, 36 hombres y 14 mujeres).

o Aleatorios sistemáticos: similar al simple, en donde como unidad del universo tiene la misma posibilidad de ser seleccionada. 

o   Aleatorios simples: cada unidad tiene la probabilidad equitativa de ser incluida en la muestra. El procedimiento más básico es el de sorteo o rifa, pero tiene una desventaja que no puede usarse cuando el universo es grande. La tabla de números aleatorios es más económica y requiere menor tiempo. Es el más fiable.

TEMA-7-TEORÍA DE LA PROBABILIDAD

PROBABILIDAD

El concepto de probabilidad es muy frecuente para comunicarnos y entendernos:

•      Ej: Las probabilidades de sobrevivir a una operación son del 50%
•   Ej: Un paciente que ingresa en el hospital “A” tiene un 15% de padecer una infección hospitalaria
•      Ej: Durante este invierno la prevalencia de enfermedades respiratorias es del 13%. 13 de cada 100 ciudadanos padece una enf. respiratoria durante el invierno.

En todos estos ejemplos se está dando la medida de ocurrencia de un evento que es incierto: sobrevivir a la operación, tener una infección hospitalaria o la ocurrencia de enfermedades respiratorias.

Se expresa mediante un número entre 0 y 1 (o en porcentajes)

En estos ejemplos, si no existe la certeza de que ocurran los hechos, existe una esperanza dimensionada y razonable, de que el hecho anunciado se vea confirmado.

Esta estimación sobre la probabilidad de ocurrencia del evento nos ayuda a tomar decisiones.

Cuanto más probable es que ocurre un evento, su medida de ocurrencia estará más próximo a 1 o al 100% y cuanto menos probable, más se aproxima al cero.

Aunque el concepto es simple, ya que se usa de manera intuitiva, su definición es complicada y tiene tres vertientes:

PROBABILIDADES SUBJETIBAS O PERSONALÍSTICAS

La probabilidad mide la confianza que el individuo tiene sobre la certeza de una proposición determinada.

Por ejemplo: los epidemiólogos se basan en la experiencia para afirmar que el próximo invierno la epidemia de gripe tendrá una probabilidad del 0,0018 (180 casos por 100.000 habitantes).

Este concepto de las probabilidades ha dado lugar al enfoque de análisis de datos estadísticos llamado “Estadística Bayesiana”.

PROBABILIDAD CLÁSICA O “A PRIORI”

Data del siglo XVIII (Laplace, Pascal, Fermat), desarrollada para resolver problemas relacionados con los juegos de azar (dados, monedas, ruletas…)

Las probabilidades se calculan con un razonamiento abstracto.

Ejemplo: no hay que lanzar el dado para saber que la probabilidad “a priori” de que salga el 6 es de 1/6=0,16.

Definición: Si un evento puede ocurrir de N formas, las cuales se excluyen mutuamente y son igualmente probables, y si m de esos eventos poseen una característica E, la probabilidad de ocurrencia de E es igual a m/N.

P(E) = 𝒎/N

Ej: La probabilidad “a priori” de que salga un As en una baraja de Póker (52 cartas) será:

·         P(As) = 4/52 = 0,769 = 7,7 %

LEY DE LOS GRANDES NÚMEROS

La probabilidad a priori de que salga un número en el dado es P(A) = 1/6 = 0,166 = 16,6 %

Inicialmente esa probabilidad real puede no cumplirse pero si repetimos muchas veces el experimento, la frecuencia relativa de un suceso A, cualquiera, tiende a estabilizarse en torno al valor “a priori”.

PROBABILIDAD RELATIVA O “A POSTERIORI”

Definición: Si un suceso es repetido un gran número de veces, y si algún evento resultante, con la característica E, ocurre m veces, la frecuencia relativa de la ocurrencia E, m/n, es aproximadamente igual a la probabilidad de ocurrencia de E

P(E) = 𝒎/n

(Si n es suficientemente grande) p = lim fr nà∞

Dicho de otra forma, si el número de determinaciones (repeticiones de un experimento aleatorio) es grande, podemos esperar que la probabilidad observada se acerque a la probabilidad teórica.

EVENTOS O SUCESOS

Diversos resultados son posibles cuando realizamos un experimento aleatorio. El conjunto de estos resultados se llama espacio muestral (S).

Suceso o evento: subconjunto de dichos resultados.

Evento unión: formado por los resultados experimentales que están en A o en B (incluyendo los que están en ambos).

Evento intersección: formado por los elementos que están en A y B.

PROPIEDADES DE LAS PROBABILIDADES

P(AUB): Cuando dos sucesos A y B se excluyen mutuamente: P(AUB)=P(A)+P(B)

P(AUB): Cuando dos sucesos A y B no se excluyen mutuamente: P(AUB)=P(A)+P(B)-P(AПB)

P(AUB): Cuando A y B son eventos independientes (la ocurrencia de uno no influye en la ocurrencia del otro): P(AПB)=P(A)xP(B)

REGLAS BÁSICAS: TEORÍA DE LA PROBABILIDAD

Las probabilidades siempre oscilan entre 0 y 1

La probabilidad de un suceso contrario es igual a 1 menos la probabilidad del suceso – P (A´)= 1-P(A)

La probabilidad de un suceso imposible es 0

La unión de A y B es:

•          P(AUB)=P(A)+P(B)-P(A П B)

La probabilidad condicionada de un suceso A a otro B se expresa:

P (A/B)= P(A П B)/P(B)                                                  Si P(B)=’0

TEOREMA DE BAYES

Expresa la probabilidad condicional de un evento aleatorio A dado B en términos de la distribución de probabilidad condicional del evento B dado A y la distribución de probabilidad marginal de sólo A.

En términos más generales el teorema de Bayes que vincula la probabilidad de A dado B con la probabilidad de B dado A.

Por ejemplo, sabiendo la probabilidad de tener un dolor de cabeza dado que se tiene gripe, se podría saber (si se tiene algún dato más), la probabilidad de tener gripe si se tiene un dolor de cabeza.

DISTRIBUCIÓN DE PROBABILIDAD EN VARIABLES DISCRETAS: BINOMIAL Y 
POISSON

DISTRIBUCIÓN BINOMIAL

La distribución binomial es un modelo matemático de distribución teórica de (la normal es con variables continuas) variables discretas

•         Cuando se producen situaciones en las que sólo existen dos posibilidades (cara/cruz; sano/enfermo…)
•        El resultado obtenido en cada prueba es independiente de los resultados obtenidos anteriormente.
•        La probabilidad del suceso A es constante, la representamos por p, y no varía de una prueba a otra. La probabilidad de `A es 1- p y la representamos por q .
•         El experimento consta de un número n de pruebas.

Mediante esta distribución se resuelven los problemas que plantean:

• Si al hacer un experimento hay una probabilidad p de que ocurra un suceso ¿Cuál es la probabilidad de que en N experimentos el suceso ocurra X veces?

o   P: probabilidad de ocurrencia; q de no ocurrencia

o   X: numero sucesos favorables

o   N: numero total de ensayos

•          Y… recordar que por definición el factorial de un número 0 es igual a 1.

DISTRIBUCIÓN DE POISSON

Poisson: médico miliar francés que estudia en el s.XIX la probabilidad de que un soldado muera en el campo de batalla por golpes de un caballo

•          También se llama la distribución de probabilidad de casos raros

Utilidad:

1. Se utiliza en situaciones dónde los sucesos son impredecibles o de ocurrencia aleatoria.
2. Permite determinar la probabilidad de ocurrencia de un suceso con resultado discreto.
3. Es muy útil cuando la muestra o segmento n es grande y la probabilidad de éxitos p es pequeña.
4. Se utiliza cuando la probabilidad del evento que nos interesa se distribuye dentro de un segmento n dado como por ejemplo distancia, área, volumen o tiempo definido.

DISTRIBUCIONES NORMALES

TIPIFICACIÓN DE VALORES EN UNA NORMAL

Extrapolando aparecen los principios básicos de las distribuciones normales y podemos tipificar valores de una normal:

•          ± 1S 68,26% de las observaciones
•          ± 2S 95,45% de las observaciones
•          ± 1,95S 95% de las observaciones
•          ± 3S 99,73% de las observaciones
•          ± 2,58S 99% de las observaciones

TIPIFICACIÓN DE LOS VALORES Y SU RELACIÓNCON LA CAMPANA DE GAUSS

La tipificación de los valores se puede realizar sí …

Trabajamos con una variable continua que:

•        Sigue una distribución normal (TLC)
•     Y tiene más de 100 unidades (LGN)

La tipificación nos permite conocer si otro valor corresponde o no a esa distribución de frecuencia

Sabemos por la forma de la curva que…

•          La media coincide con lo más alto de la campana: 8
•          La desviación típica es de 2 puntos

o   El 50% tiene puntuaciones>8

o   El 50% tiene puntuaciones<8

o   Aproximadamente el 68% puntúa entre 6 y 10

§  media +/- 1 desviación típica: 68%

·         8+/-1: 6-10

§  Media +/- 2 desviación típica: 95%

·         4-12

§  Media +/- 3 desviación típica: 99%

·         2-14

TEMA-6-REPRESENTACIÓN GRÁFICA DE LA INFORMACIÓN

REPRESENTACIONES GRÁFICAS

Forma rápida de comunicar información numérica (frecuencias)

Son la imagen de las ideas (barras, histogramas, sectores...)

Complementan el análisis estadístico, aumentando la información y ofreciendo orientación visual

No reemplaza a las medidas estadísticas que deben ser calculadas

Normas básicas:

•          Visualmente claros
•          Claramente descritos en pie de figura y en texto
•          Representar gráficamente las conclusiones del estudio
•          Evitar gráficos confusos, no sobrecargarlos

REPRESENTACIÓN GRÁFICAS MÁS EMPLEADAS

VARIABLES CUALITATIVAS:

·      

•         Gráfico de sectores (dicotómicas o policotómicas con pocas categorías)

o   El área de cada sector circular es proporcional a la frecuencia (absoluta o relativa) de las categorías de la variable.

o   No usar con variables ordinales.

o   No recomendables para más de 3 ó 4 categorías.

o   Sólo muestra una variable a la vez. Si se quiere hace comparaciones se tienen que hacer dos diagramas de sectores

o   Errores en gráficos de sectores

§  Variable policotómica (muchas categorías)

§  Variable ordinal

•          Gráfico de barras (policotómicas)

o   Las frecuencias absolutas o relativas de todas las categorías de una variable cualitativa se muestran fácilmente con este tipo de gráfico

o   Cada barra representa una categoría y su altura la frecuencia (absoluta o relativa)

o   Las barras deben estar separadas

o   Es importante que el eje Y empiece en la frecuencia 0

o   Errores

§  Se comparan frecuencias absolutas y no son comparables

§  Se trata de una variable cuantitativa. Es preferible un histograma (polígono de frecuencias, tronco y hojas…) y un resumen numérico (media, desv.típica)

•          Pictogramas (policotómicas) (igual que diagrama de barras pero con dibujo)

VARIABLES CUANTITATIVAS:

·      

•            Gráfico de barras (sólo para variables discretas con bajo rango de valores)
•           Histogramas (variables continuas)

o   Sucesión de rectángulos contiguos construidos sobre una recta.

o   Representa a una variable continua con sus datos agrupados en intervalos.

o   La base de cada rectángulo representa la amplitud de cada intervalo y la altura está determinada por la frecuencia.

o   Cada intervalo representado en el histograma ocupa un rectángulo

àIgual que diagrama de barras en cuanto al tipo de frecuencias que se pueden utilizar. La diferencia: es para variables CONTINUAS. Si la amplitud del intervalo es la misma, elevaremos columnas UNIDAS, a altura la frecuencia correspondiente. Si la amplitud del intervalo es diferente, el área del rectángulo columna será proporcional a la frecuencia representada.

o   Errores:

§  Se ha realizado en realidad un diagrama de barras, inapropiado para una variable continua.

§  No se han tenido en cuenta las diferentes amplitudes de los intervalos.

•          Polígonos de frecuencia (variables continuas)

•          Gráfico de tronco y hojas (variables continuas)

o   Híbrido entre tabla e histograma: Nos muestra la forma de la distribución y los valores de la variable

o   Cada dato de la serie se divide en dos partes: el tronco (decenas) y la hoja (unidades)

DATOS BIDIMENSIONALES Y MULTIDIMENSIONALES:

·        

•      Tendencias temporales
•          Nubes de puntos (scatter plot)

o   Para representar el comportamiento de dos variables continuas en un grupo de individuos.

o   En el eje “x” se representa la variable independiente y en el eje “y” los valores de la variable dependiente.

o   La imagen del diagrama nos da una posible idea de la correlación entre las dos variables

•           Otros gráficos multidimensionales (diagramas de estrellas…)

o   Para representar un conjunto de variables cuantitativas y comparar entre diferentes unidades de análisis (individuos o conglomerados).

o   Cada variable representa un vértice del diagrama de estrella.

o   Gráficamente da una idea del comportamiento conjunto de las variables estudiadas.

o   También permite comparativas con un “gold standard”.